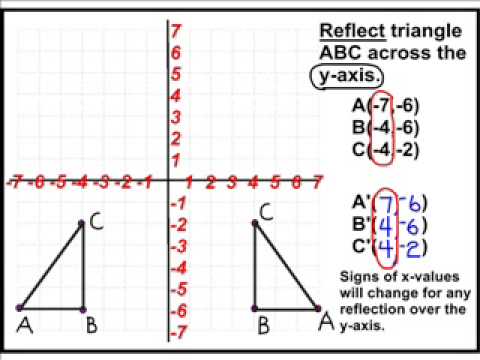
Transformation Rule For Reflection
Rules coordinate reflections ry onlinemathlearning worksheets mathematics What is the rule for the reflection? a. ry=x(x, y) → (–y, –x) b. ry=–x 10 math problems: transformation: reflection
What is the rule for the reflection? A. ry=x(x, y) → (–y, –x) B. ry=–x
Geometric transformations & their rules Transformation level reflection Reflection transformation
Axis rules
Reflection transformation geogebraTransformation reflections notation What is a transformation?Axis reflection over transformation.
Transformation notationReflection nagwa Describing transformations reflection and rotation gcse maths revisionReflection transformation matrix.

Transformation: reflection over the y-axis
Reflection(a type of transformation) – geogebraReflection matrix transformation axis Reflection transformations axis math rules across mathematics reflections algebra performing review translations worksheets rotations j1xReflection rules (x-axis, y-axis, y=x, y=-x).
Reflection mirror symmetry axis onlinemathlearningTransformations maths describing reflection rotation gcse practice revision exam paper O level mathematics topic transformation-reflection part 2Transformations reflections.
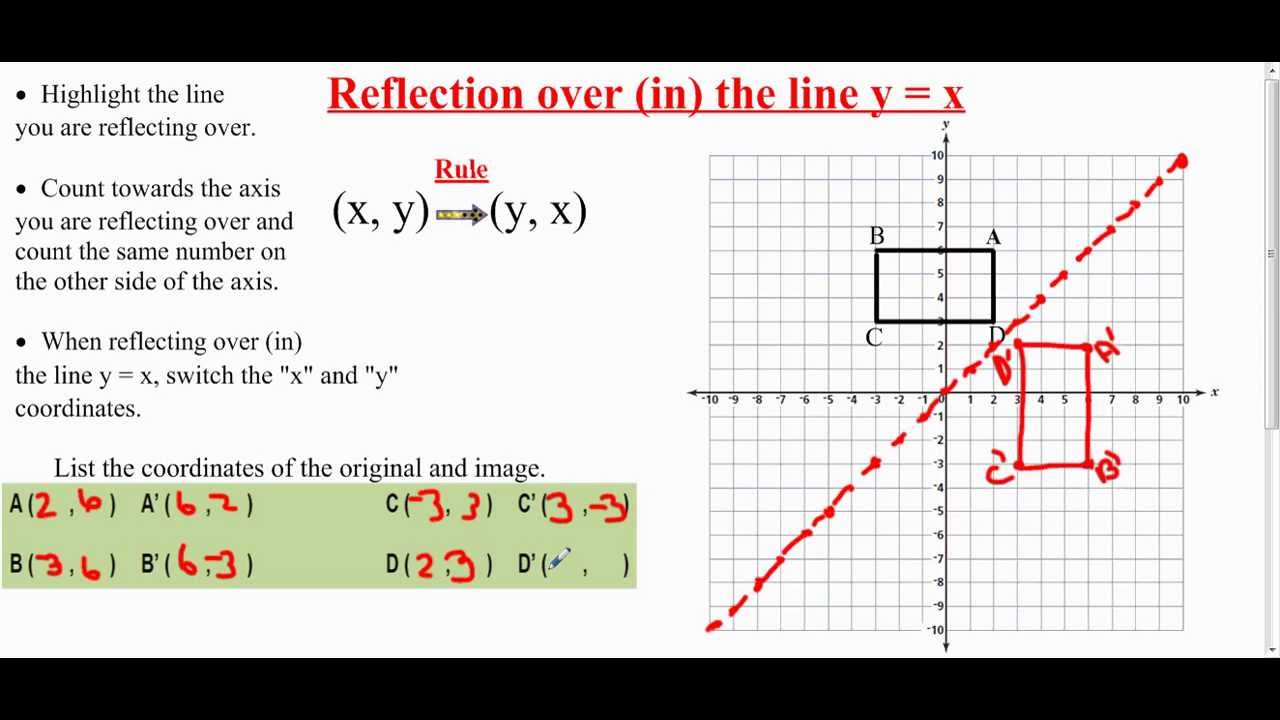
Transformations reflections
Reflection transformation (solutions, examples, videos)What does the x mean in a math equation Reflection transformation formulae example geogebra typeReflection coordinate rules transformation rule axis math transformations line reflected over across plane geometry rotation reflect coordinates origin examples triangle.
Algebraic representations reflections rules transformations rotation reflection examples worksheet onlinemath4allLesson video: function transformations: reflection Axis graph reflection reflecting transformation matrix line examples horizontal vertical onlinemath4allReflections transformations.

Reflection transformation matrix
Algebraic representations of transformations worksheetAxis reflect reflection transformations coordinates coordinate definition Reflections transformations.
.